次元削減の中で最もよく使用されているであろう主成分分析(PCA)の使い方を紹介します。
csvデータを主成分分析したい場合には役立つサンプルコードを載せています。本コード参考に少しアレンジを加えれば簡単に分析できると思います。
今回の分析データは、csv形式で作成したプロ野球のチーム成績(2020/10/11時点)で、それを読み取ってチームの傾向をマップ表示してみました。
結果を早く見たい方は下から見たほうがよいです。
主成分分析(PCA)とは
主成分分析(PCA…Principal Component Analysis)は、次元削減手法の中では歴史が長く様々な分野で使用されおり、複雑なデータを簡単に可視化することができます。
次元削減の手法には
- 重要な要素・項目以外は破棄して、次元数を減らす
- 元のデータから新たな変数を合成して次元数を減らす
の2通りがあり、PCAは2番目の手法になります。
削減後の軸は主成分と呼ばれます。
各主成分の重要度の割合を寄与率といい、元のデータをどれくらい説明しているかを表します。
また第一主成分から各寄与率を加算したものを、累積寄与率といいます。
Pythonでの主成分分析(PCA)をPythonで

機械学習ライブラリscikit-learnを使用します。
分析者が用意すべき要素は、入力するデータ、削減後の次元数です。
今回は独自データを主成分分析しますが、用意しなくても
scikit-learn内に、サンプルデータ(アヤメのデータ)が用意されているのでそれを使用して動作を確認できます。
また入力データは、各要素ごとに平均0、分散1になるよう標準化をするのが一般的なようです。
サンプルコード
入力データ:プロ野球球団のチーム成績
2020/10/11現在の各プロ野球チームの成績を主成分分析し、2次元のグラフに表示します。
入力データはcsv形式で作成し、それを読み込んで分析します。
以下が今回の入力データです。
データの項目は順番に、得点、失点、本塁打、盗塁、打率、防御率になっています。

またセリーグ、パリーグで、選手起用に関するルールが若干異なるので別々に分析します。
ソースコード
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# 読み込むファイル名
csvfile_name = '20201011_CentralLeague'
#csvfile_name = '20201011_PacificLeague'
# データの読み取り
data = np.loadtxt(csvfile_name+'.csv', delimiter=',', usecols=range(1,7))
print('◆読み込みデータ :'+csvfile_name+'.csv')
print('[ 得 点 ] [ 失 点 ] [ 本塁打 ] [ 盗 塁 ][ 打 率 ][ 防御率 ]')
print(data)
# データの正規化(前処理)
print('◆標準化データ')
scaler = StandardScaler()
scaler.fit(data)
data_norm = scaler.transform(data)
print(data_norm)
###### PCA実施 ######
# n_comps:次元削減後の要素数
n_comps = 2
pca = PCA(n_components = n_comps)
pca = pca.fit(data_norm.data)
rslt = pca.transform(data_norm.data)
###### PCA結果表示関連 ######
print('◆PCA結果')
print(rslt)
# 寄与率表示
print('+寄与率[%]')
print(pca.explained_variance_ratio_)
print('+各主成分の構成')
print(pca.components_)
# グラフ描画
plt.scatter(rslt[:,0],rslt[:,1],marker='o')
plt.title(csvfile_name)
plt.xlabel('PC1')
plt.ylabel('PC2')
# csvからラベル取得
labels = np.genfromtxt(csvfile_name+'.csv', delimiter=",", usecols=0, dtype=str)
# ラベル表示
for label, x , y in zip(labels, rslt[:,0], rslt[:,1]):
plt.annotate(
label,
xy = (x,y), xytext = (40,-20),
textcoords = 'offset points', ha = 'right', va = 'bottom',
bbox = dict(boxstyle = 'round,pad=0.5', fc='yellow',alpha=0.5),
arrowprops = dict(arrowstyle='->',connectionstyle='arc,rad=0')
)
# グラフ保存
plt.savefig('PCA_Result_'+csvfile_name)
plt.clf()
実行時の出力は以下のようになります(一例としてパリーグのみ表示)。
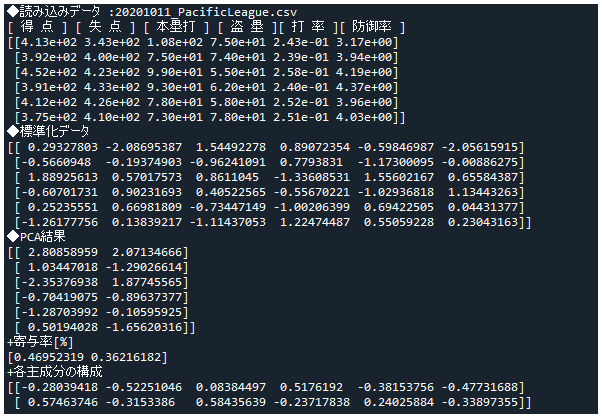
結果分析
結果のグラフの軸に「主に」影響を与えている要素を矢印で示しています。少なからず他の要素も影響を与えているため並びに違和感を感じる場合は「各主成分の構成」をよく確認してみてください。
パリーグ
グラフから読み取れることは、ホークスとイーグルスが正反対でありながら視点によっては似ていること、他球団はその2球団に比べるとある程度似た特色ということでしょうか。
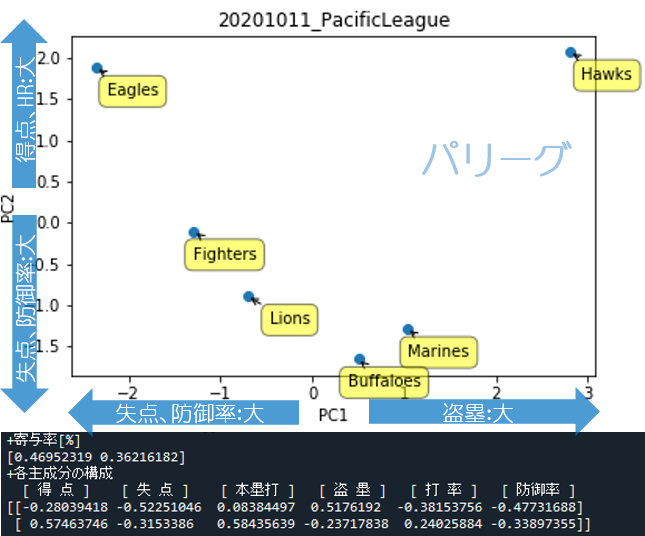
寄与率の合計は83%(=46.9+36.2)なので、各チームの特色はおおよそ8割このグラフ上で表現されていることになります。
「各主成分の構成」から以下のことが読み取れます。
- 横軸(1行目):盗塁が大きいと+方向へ、失点・防御率が大きいとー方向へ
- 縦軸(2行目):得点・本塁打が大きいと+方向へ、失点・防御率が大きいとー方向へ
第一主成分(横軸)より、盗塁数と失点、防御率を中心に分析すると特色が出るようです。
グラフの上に位置するほど攻撃的であるが、ホークスとイーグルスでは、失点数と盗塁数の差から横方向では離れています。
セリーグ
グラフから読み取れることは、ドラゴンズが異質であること、カープとスワローズが似ていることあたりでしょう。
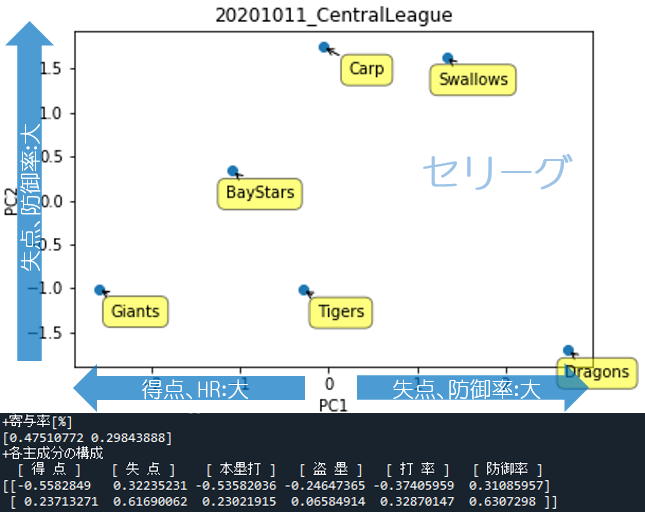
寄与率の合計は77%(=47.5+29.8)なので、各チームの特色はおおよそ8割このグラフ上で表現されていることになります。
寄与率を見る限り、縦軸(第二項PC2)は29.8%であり、パリーグの縦軸と比べるとうまく特徴を表現できていないようです(パリーグのPC2は36.2%)
「各主成分の構成」から以下のことが読み取れます。
- 横軸(1行目):失点・防御率が大きいとやや+方向へ、得点・本塁打が大きいとー方向へ
- 縦軸(2行目):失点・防御率が大きいと+方向へ、打率も高いとやや+方向へ
第一主成分(横軸)より、得点、HR数と失点、防御率を中心に分析すると特色が出るようです
得点とHRが異様に少ないドラゴンズの異質さが際立っているほか、攻守において高次元なジャイアンツも特色が強く中心から外れていますね。
最後に
ライブラリのおかげで主成分分析は簡単に実施できるうえに、結果が見やすいので便利です。
今回のプログラムを少しいじれば任意のcsvファイルのデータを主成分分析できるので活用してみてください。
今後も何かネタがあればやってみようと思います。というか定期的にチーム分析を続けようかなと思ったり。
今回は相関の強いパラメータ(得点とHR、失点と防御率など)が多かったので縦軸と横軸の成分が似てしまった気もするので、次回(未定)は入力データをより多様にすべきかなと思います。
(以下追記)
2021年度シーズン前半戦の結果をPCAした結果が以下記事です。入力データを少し見直しています。
気なる方はぜひご覧ください。




コメント